Welcome to my blog about mathematics. My name is Daniyar Omarov. I am studying at Nazarbayev
University and majoring in Mathematics. Also,
I am a member of the local mathematics club, where we solve interesting
questions and conduct seminars on various topics. Mathematics fascinates me because
one can accomplish extraordinary and amazing things using various theorems and facts.
Have you ever thought how to evaluate infinite area? In my first post I will explain the technique of improper integral, which mathematicians use to estimate areas that go to infinity. To make explanation clearer, I will start by clarifying what is definite integral.
Have you ever thought how to evaluate infinite area? In my first post I will explain the technique of improper integral, which mathematicians use to estimate areas that go to infinity. To make explanation clearer, I will start by clarifying what is definite integral.
Figure 1. Definition of Definite Integral. Source: Anton,
Bivens, and Davis 2013, 354.
The definition of the definite integral is complicated as it
can be seen in Figure 1. However, more understandable explanation is that
definite integral is the area under closed interval.
To better understand the concept of definite integral consider simple example, when function of x is equal to x, that is f(x)=x. (Graph 1 and Figure 2).
Graph 1. Area of the function Figure 2. Calculation of the Area
From the calculation above we find that the area under the line f(x)=x is equal to 2 (units squared) between x=0 and x=2. This can also be proved using the formula for finding the area of a right triangle, where opposite and adjacent sides are both equal to 2 (units). According to the formula: A= (B*C)/2=(2*2)/2=2 (units squared). Consequently, area acquired from our integration is correct.
Now we move to the improper integral. Anton et. al. defines it as the definite integral with infinite intervals or infinite discontinuities.
Firstly, consider integrals over infinite intervals.
Graph 2 illustrates the definite integral with infinite interval. In order to calculate area under that graph the combination of previous method and limits is used.
Graph 2. Improper Integral with Infinite Interval. Source: Anton, Bivens, and Davis 2013, 548.
Next, consider the improper integrals whose integrands have infinite discontinuities.
For reference, infinite discontinuities are the points on the graph where f(x) or x do not exist. For instance, if f(x)=1/x, then the point of discontinuity is x=0 because f(0)=1/0 does not exist.
Graph 3 shows example of improper limit with the point of discontinuity.
Graph 3. Improper Integral with Infinite Discontinuity. Source: Anton, Bivens, and Davis 2013, 551.
The following video explains the concept of improper integral in depth.
Video 1. Explanation of the Improper Integral. Link
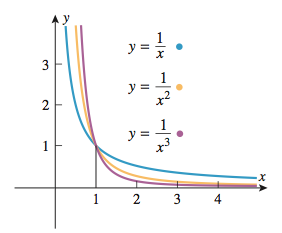
After all these theories we proceed to the most interesting part. Graph 4 demonstrates three similar graphs that have infinite integrals.
Graph 4. Examples of Improper Integrals. Source: Anton, Bivens, and Davis 2013, 549.
Looking at the Graph 4, one might assume that three areas under the curves between x=1 and x=∞ cannot be estimated because functions go to infinity. The following calculations show whether the assumption is correct:
Figure 3. Calculation of the Area of the function f(x)=1/x. Source: Anton, Bivens, and Davis 2013, 549.
Figure 4. Calculation of the Area of the function f(x)=1/x2. Source: Anton, Bivens, and Davis 2013, 548.
Figure 5. Calculation of the Area of the function f(x)=1/x3. Source: Anton, Bivens, and Davis 2013, 549.
Surprisingly, only the f(x)=1/x function`s area is equal to infinity. In contrast, the remaining two functions have exact values for their areas. These calculations show that even abstract concepts can be estimated in some cases. This is one of the examples illustrating that mathematics is full of paradoxes and unexpected outcomes.
Additional links for further research:
Improper Integral with Two Infinite Bounds. Link
Divergent Improper Integral. Link
Improper Integrals in Theoretical Aerodynamics. Link
Improper Integrals on Time Scales. Link
Reference List
Anton, Howard, Irl Bivens, and Stephen Davis. Calculus: Early Transcendentals. 10 ed. Asia: John Wiley & Sons Singapore Pte.Ltd, 2013.
Bohrer, Martin, and Gusein Sh. Guseinov. "Improper Integrals on Time Scales." Dynamic Systems an Applications 12 (2003): 45-65. http://web.mst.edu/~bohner/bimadsa/bohner.pdf (accessed September 26, 2014).
"Divergent improper integral." Khan Academy. https://www.khanacademy.org/math/integral-calculus/indefinite-definite-integrals/improper-integrals-tutorial/v/divergent-improper-integral (accessed September 26, 2014).
"Improper integral with two infinite bounds." Khan Academy. https://www.khanacademy.org/math/integral-calculus/indefinite-definite-integrals/improper-integrals-tutorial/v/improper-integral-with-two-infinite-bounds (accessed September 26, 2014).
"Introduction to improper integrals." Khan Academy. https://www.khanacademy.org/math/integral-calculus/indefinite-definite-integrals/improper-integrals-tutorial/v/introduction-to-improper-integrals (accessed September 26, 2014).
Mangler, K. W. . Improper Integrals in Theoretical Aerodynamics. London: Nine ShIllings Net, 1952. http://naca.central.cranfield.ac.uk/reports/arc/cp/0094.pdf (accessed September 26, 2014).


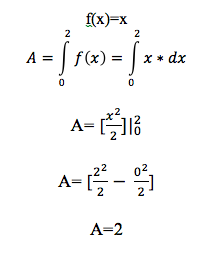


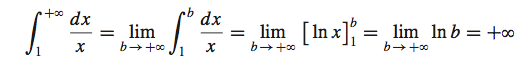


No comments:
Post a Comment